自十九世纪雷诺的管流实验以来,线性稳定的剪切层流向湍流的转变或亚临界转捩机制一直困扰着物理学家、流体力学家和数学家。亚临界转捩过程的主要特征之一是存在间歇的湍流结构,这些多尺度结构的局地性和强非线性给理论研究带来困难,比如迄今仍缺乏对湍流结构对流速度选择机制的定量研究。对于二维槽流的亚临界转捩,其对应的局地结构是波包[1]:其流向尺度比槽宽大一个量级,内部的主要特征是在近壁处各有一列小涡旋结构 (如图1a)。
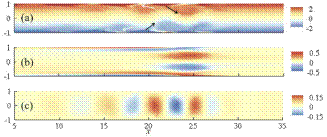
图1. 槽流中局地波包的 (a) 瞬时涡量场、(b) 平均流修正部分的涡量、(c) 脉动流场的法相速度。Re=2400.
近日,33678新甫京国际品牌力学与工程科学系陶建军课题组通过数值模拟、稳定性分析和动力学模型,回答了关于槽流转捩的几个根本问题:近壁小涡漩结构的产生和传播机制是什么?局地波包的自维持机理是什么?其对流速度从何而来?二维槽流亚临界转捩的阈值雷诺数是多少?转捩的起始是连续型的还是非连续型的?
首先,在平移坐标系中将数值模拟所得的局地波包结构的速度场分解为三部分,即基本流、平均流修正部分和脉动部分。如图1(b)所示,在平均流修正流场中存在一个有趣的现象:在波包的下游头部存在一个涡对。该涡对对局地波包的传播与自维持机制有着决定性的影响。其次,通过对平均流沿程速度剖面的稳定性分析,发现(1)在涡对处存在绝对不稳定区,可产生有限幅值的行波模态;其上游边界处的绝对频率同数值模拟所得脉动场主控整体频率(global frequency)相符。(2)空间模式行波模态的传播方向、空间幅值衰减率和流向波数均同数值模拟脉动场相符(见图2)。因此,波包涡量场中两列近壁涡旋结构所代表的脉动成分实质是由当地平均流色散关系决定的行波模态。
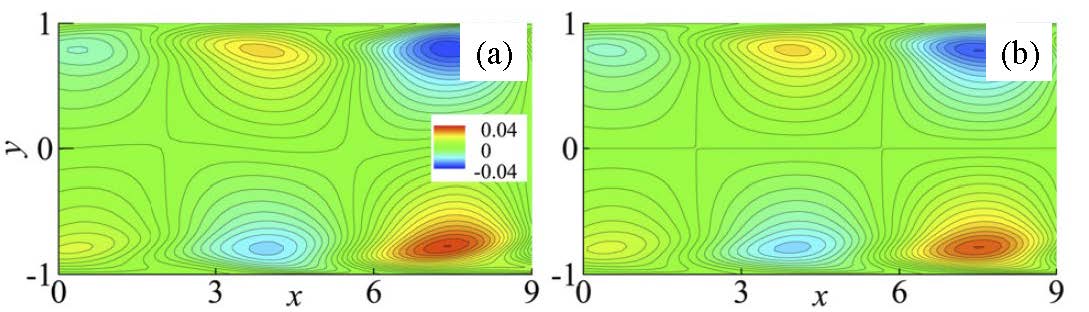
图2. (a) 数值模拟所得波包流向脉动速度等值线,(b) 稳定性理论所得行波模态流向速度等值线。Re=2400.
再次,周期变化的脉动场对应的雷诺应力会产生漂流(streaming)从而影响平均流。通过分析脉动场的雷诺应力分布,发现在波包下游头部的中线处会形成指向下游的漂流,而在近壁处漂流会反转为指向上游,即头部处的漂流会强化涡对流动(图3)。这些结果给出了槽流中局地波包的自维持机制,即波包中的行波和头部的涡对是共生的关系:涡对造成的平均流修正可产生有限幅值的行波,而行波的雷诺应力有利于维持涡对、防止其因粘性扩散与耗散而衰减掉。

图3. 脉动行波(FW)的雷诺应力导致的漂流示意图。
进一步地,通过将平均流修正场的压力梯度用流向速度齐次阶导数来表达,封闭了中线处的流向动量方程,从而建立了描述中线平均流修正流场的KdV形式的一维动力学模型。模型所得的解析的孤立波解的最大值同数值模拟所得的涡对中线处数据相符,从而定量地说明局地波包的对流速度是由波包头部涡对的孤立波速度决定的。
亚临界转捩的精确预测与控制之所以困难,主要是由于转捩起始对外部扰动的形式与强弱敏感。不同于以往研究中用随机扰动或周期行波作初始扰动,本文采用孤立的波包作为初始扰动,获得了迄今最低的转捩雷诺数或转捩阈值,Re = 2330.5 ± 0.5。更重要的,在此雷诺数时单位长度的波包数或阈值波包密度并不是零,而是有限值0.022,从而说明二维槽流的亚临界转捩是非连续型的。
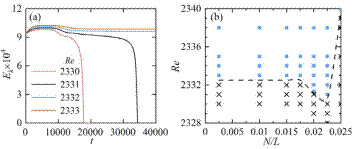
图4. (a) 扰动动能随时间的演化。初始流场含波包数N = 8。(b) ■和x符号分别表示在40000时间单位内初始波包存活与衰减掉的算例。计算域长度L = 400。
相关结果在Physics of Fluids作为Letter发表[2],作者包括力学与工程科学系博士生肖越和张林森。该研究得到国家自然科学基金重大研究计划重点项目资助。
[1] J. Jimenez, “Transition to turbulence in two-dimensional Poiseuille flow” J. Fluid Mech. 218, 265–297 (1990).
[2] Y. Xiao, J.J. Tao, L.S. Zhang “Self-sustaining and propagating mechanism of localized wave packet in plane-Poiseuille flow” Phys. Fluids, 33, 031706 (2021). https://doi.org/10.1063/5.0042346










