复杂系统是由大量相互作用并彼此演化的组成成分所构成的系统,这些系统广泛存在于工程技术与自然界等的各个领域(如群体无人机、智能电网、交通网络系统,生态系统,神经系统等)。理解复杂系统的动力学行为是多领域研究人员长期广泛关注的科学问题。2021年,Syukuro Manabe、Klaus Hasselmann和Giorgio Parisi三位科学家凭借对理解复杂系统的开创性贡献获得了诺贝尔物理学奖。
平衡点稳定性是复杂系统动力学分析中的一个重要概念,它衡量系统平衡态在受到外界扰动后恢复到受扰前状态的能力。对于不稳定的系统,微小的扰动便可使系统远离平衡状态,从而引起系统失衡。已有的关于复杂系统稳定性的研究成果往往假定系统中智能个体间的交互作用是瞬时完成的,系统中任一个体的变化会立即对其他作用个体产生影响(图1a)。然而,由于真实系统中信号的传输、个体对信号的响应及处理时间等因素的存在,个体间交互作用往往具有一定的时间延迟,即时滞:个体状态的变化需要在一定的时间之后才会对其他个体状态产生影响(图1b)。真实复杂系统中种类繁多的智能个体,以及个体间多维度、多层次、非线性的交互作用使得时滞复杂系统的稳定性分析成为自动控制、系统科学、人工智能、生物学等多学科交叉领域的重要难题。
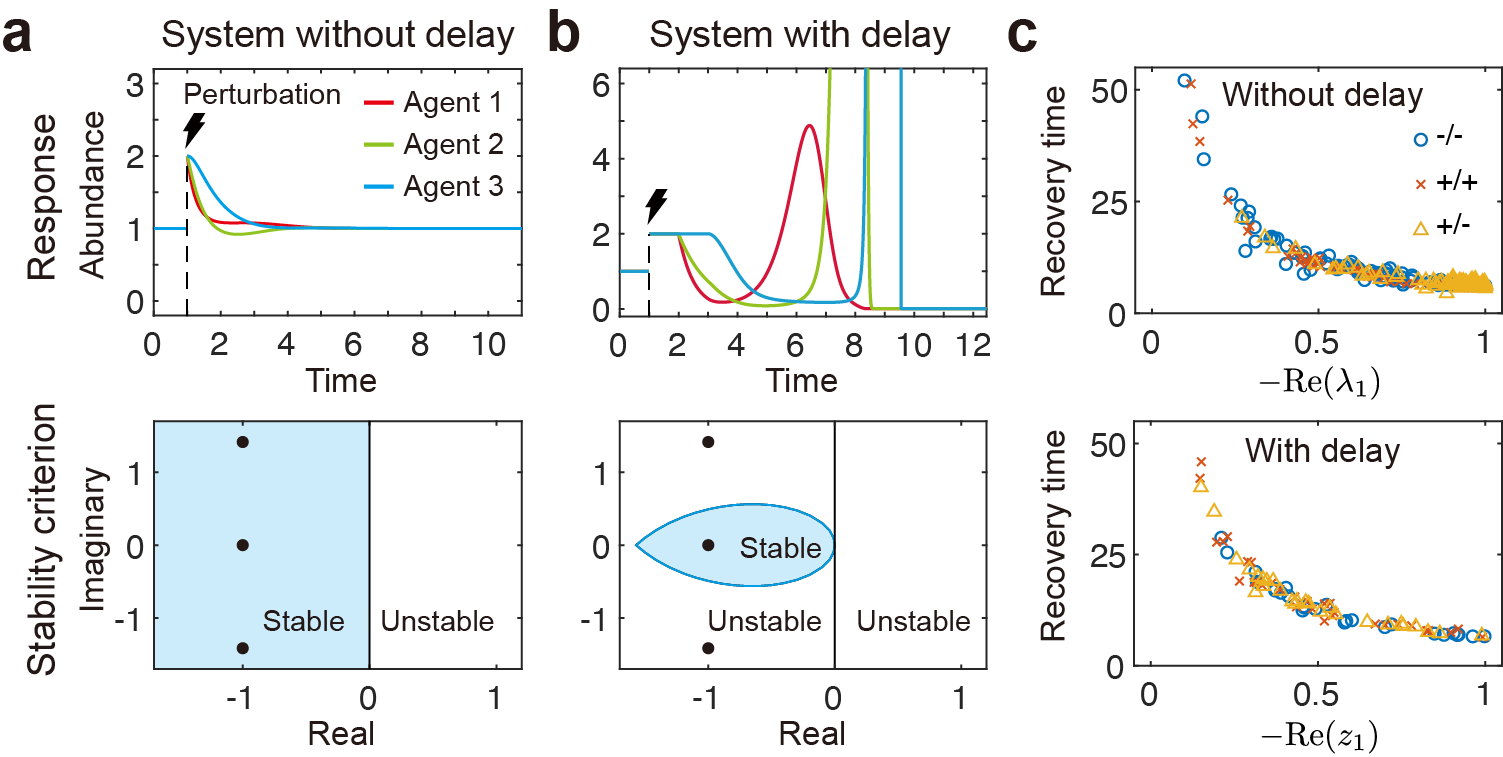
图1. 不同类型系统(无时滞系统与时滞系统)动力学及其稳定性指标
最近,李阿明课题组在这一问题的研究中取得了重要进展,他们建立了时滞复杂系统稳定性理论分析框架,提出了一种估计时滞复杂系统稳定性的理论方法。课题组发现,仅用传统的无时滞系统的稳定性分析框架不能充分反映时滞系统稳定性特征;利用随机矩阵理论与非线性动力学稳定性等理论,课题组给出了时滞系统稳定性衡量指标(图1c)。研究发现,对于含有多种交互类型(如生态系统中竞争、合作以及负反馈等)的复杂系统,时滞强度的增加将首先增强系统的稳定性,而后降低系统的稳定性,最终使得系统失去稳定性;另外,研究还发现交互多样性可以提升系统稳定性。该研究成果有助于深入理解真实复杂系统的动力学行为,为建立有效的复杂系统调控策略提供了理论基础。相关工作以“Time delays modulate the stability of complex ecosystems”为题于2023年8月17日发表在国际期刊Nature Ecology & Evolution。
另一重要发现围绕稳定性理论在刻画复杂系统动力学短期行为的不足展开。通常,稳定的系统在受扰后可能会立刻减弱(图2a)或放大(图2b)这一扰动;当扰动被放大时,可致使系统瞬态性能失效,诱发系统内潜在故障或缺陷,增大系统崩溃的风险。基于此,课题组提出并研究了系统对外界扰动的最大初始放大率问题,即系统反应性(图2);当最大初始放大率为正时,有一部分扰动会被放大,相应的系统便被称为“具有反应性”(图2b, d)。
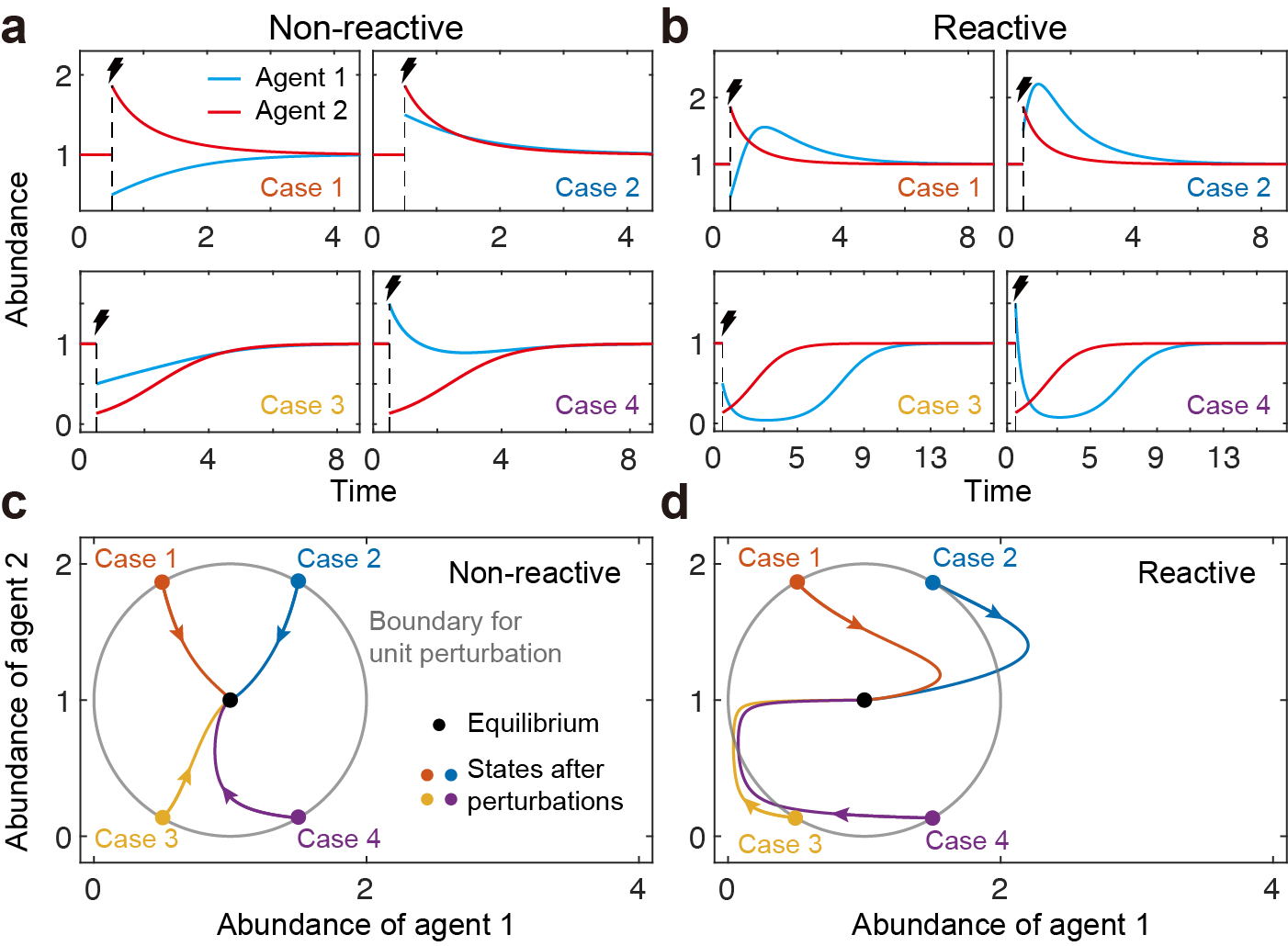
图2. 反应性刻画了系统受扰后的瞬时响应
课题组首先建立了复杂系统反应性分析的理论模型,探索了不同交互类型下复杂系统反应性问题。研究发现,智能个体间的合作与竞争作用倾向于提升系统的反应性,而个体间的负反馈作用则倾向于降低系统的反应性。针对系统稳定性与反应性之间的定量关系,课题组发现具有混合交互作用以及负反馈主导的系统将更有可能呈现出反应稳定状态,并通过对真实系统的数据分析验证了这一结论;研究还指出,在持续扰动下,反应稳定系统相较于非反应稳定系统更容易发生崩溃。该研究成果揭示了复杂系统受扰动力学的短期行为,弥补了传统稳定性概念在对复杂系统动力学短期行为刻画方面的不足。相关工作以“Reactivity of complex communities can be more important than stability”为题于2023年11月8日发表在国际期刊Nature Communications。
33678新甫京国际品牌2020级博士研究生杨浴光为上述两篇论文的第一作者,李阿明为通讯作者,合作者包括曼彻斯特大学生物系Katharine Z. Coyte助理教授(论文一共同通讯作者)和牛津大学生物系Kevin R. Foster教授(论文二共同通讯作者)。本研究得到科技部重点研发计划青年科学家项目,国家自然科学基金,北京市科技新星计划等的支持。










