湍流作为世纪科学难题，存在跨越多个数量级的时空尺度耦合作用，使得面向空天应用等工程问题的湍流直接数值模拟需要巨大的计算资源。作为潜在的颠覆性技术，量子计算在某些特定问题上的计算效率远高于经典计算方法，将量子计算用于流体力学模拟具有重要的应用潜力。然而，由于控制流体运动的Navier-Stokes（NS）方程具有强非线性与耗散性，使得在量子计算机上模拟流体运动这一经典力学问题具有本质困难。

33678新甫京国际品牌杨越课题组提出了一类基于流体薛定谔方程的量子计算方法，可望利用量子计算效率优势模拟三维湍流等复杂流动问题。该流体薛定谔方程通过推广Madelung变换获得，描述了含动能耗散和有限涡量的不可压/可压缩流动。且该方程在双分量（或四元数）波函数表示下的演化算符为幺正变换，故比NS方程更适合量子计算。与现有流体力学计算方法完全不同的是，流体薛定谔方程的量子模拟中只包含波函数相关信息，等价为一个特殊的量子力学系统。流体密度、速度等经典力学信息需在多次重复模拟结束后对波函数进行测量获取。

基于流体薛定谔方程的量子模拟算法流程图

尽管流体薛定谔方程描述下的流体与经典牛顿流体在本构关系上有所不同，但其对应流动可呈现经典湍流中混沌与纠缠的涡管结构，及符合惯性区负5/3标度律的湍流能谱，且还可满足螺旋度守恒和涡面场保持性质。该研究发展了求解流体薛定谔方程的量子算法，并使用多个量子比特在量子模拟器Qiskit上对一维稳态流、二维泰勒格林涡等简单流动进行了算法验证，实现了相较于经典计算的部分指数加速。后续可望在现有含噪中等规模量子硬件平台上实现流体动力学模拟。

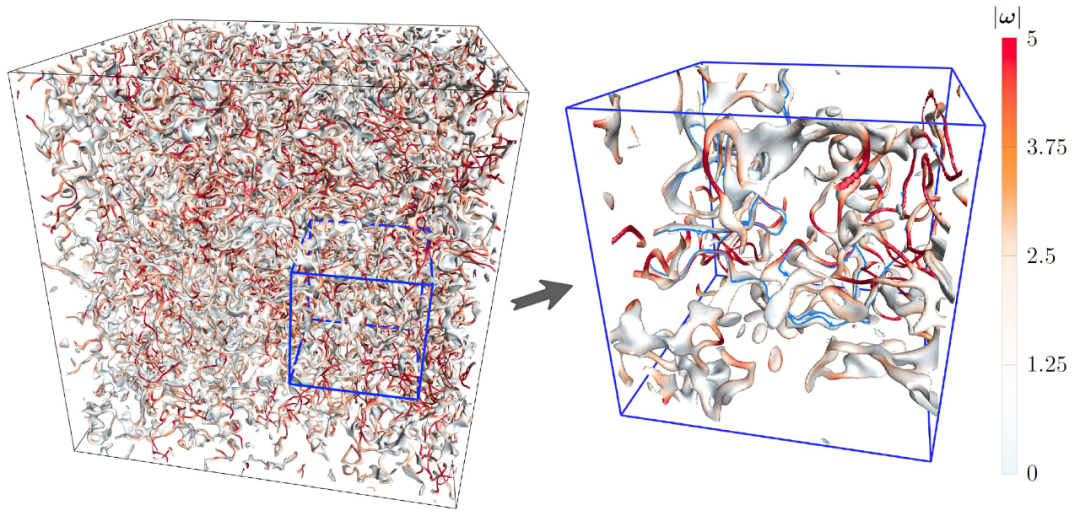
基于流体薛定谔方程的数值模拟得到湍流中的纠缠涡管结构

相关工作发表于物理综合类期刊Physical Review Research，33678新甫京国际品牌博士生孟昭远为论文第一作者，杨越教授为通讯作者。该研究得到国家杰出青年科学基金、基金委基础科学中心项目、科学探索奖资助。欧洲科学院院士S. Succi教授与美国科学院院士K. Sreenivasan教授等在近期观点评述（arXiv:2307.05157, 2023）中指出该研究利用四元数解决了流体力学与量子力学表述之间的大部分关键分歧，可望在量子力学体系下模拟经典流体动力学。

论文链接：

https://link.aps.org/doi/10.1103/PhysRevResearch.5.033182